During the last couple of months, I have been logging onto Zwift at random occasions, both day and night, to write down the number of Zwifters in each world. The Companion app gives the total number of Zwifters, so it’s possible to calculate the number of Zwifters in the worlds not on rotation as well.
Why Is This Interesting?
Having numbers through different times of day, and across longer periods, can be regarded as customer data and be used to predict customers’ preferences, desires, and future behaviors. This is a central component of data-driven marketing and probably the type of data Zwift use to plan further expansions and the road ahead.
Zwift does of course collect detailed continuous data on many aspects of use. Not only which nationalities are riding and where they’re riding but also how long people spend in each world, their favorite courses, and where they push the most wattage. A limited dataset cannot give very detailed information on customer data but can still be analyzed for interesting trends. It might be used to at least answer some questions on the average Zwifter’s preferences and behavior. Here I have applied some flexible statistical models that correlate data nonlinearly and control for several effects at the same time to the data I extracted. The point was to shed some light on a few of the most basic questions.
When Does the Average Zwifter Ride?
Whether you like to outsprint slower riders while hanging on to faster ones, or you think some worlds are getting too busy, it can be useful to know when the number of Zwifters peaks.
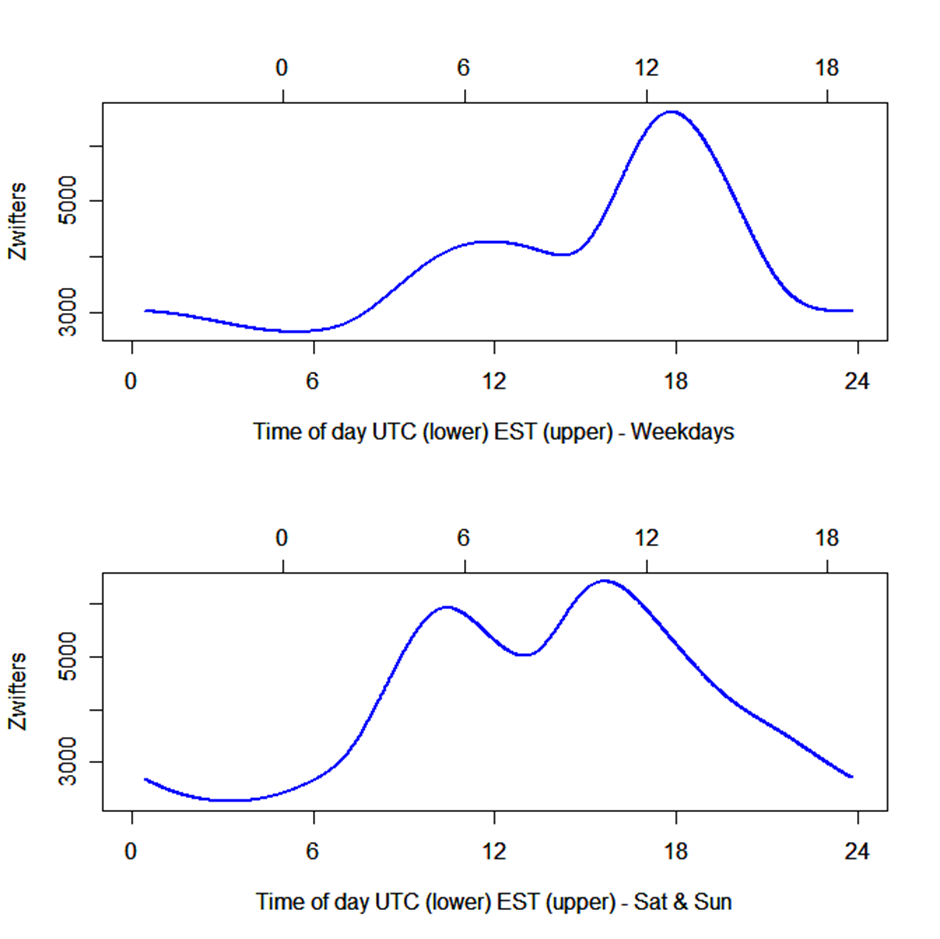
The figures above show the expected number of Zwifters through a 24h period in Watopia in the middle of December. The expected absolute number of Zwifters in the other worlds on rotation will be different, but the trend through the 24h period is here modeled as the same no matter where. The model did also include a trend through the period, so different dates will also have different absolute numbers.
The patterns are different during weekdays and weekends. Not surprisingly, on Saturday and Sunday the peak period is wider, maybe with two peaks at around 10:30 UTC and another at nearly 16:00 UTC. During weekdays, the most prominent peak is the “European afternoon” peak at 17:49, while the earlier peak is less prominent. In addition, the weekend average is 361 riders more than during weekdays. The time with the lowest activity is around midnight EST (or Zwift Standard Time, since that’s when the worlds are changing). If we assume that most people are Zwifting after work on weekdays (1700-2000), the patterns of Zwifters throughout the day would best fit Europe and have least activity in the US and East Asia.
What is the Most Popular World?
The average number of riders in each world could be regarded as a popularity index. So, here is the list with the average number of Zwifters in parenthesis from lowest to highest when time of day and date is corrected for:
| Rank | World | Average # of Zwifters | Days in Rotation in period | # of Routes |
| 10 | Paris | 838 | 10 | 2 |
| 9 | Worlds not on rotation | 1131 | Always available | NA |
| 8 | Yorkshire | 1213 | 18 | 5 |
| 7 | Richmond | 1251 | 13 | 3 |
| 6 | Innsbruck | 1691 | 17 | 5 |
| 5 | New York | 1718 | 21 | 11 |
| 4 | London | 2962 | 14 | 13 |
| 3 | France | 3622 | 10 | 7 |
| 2 | Makuri | 3751 | 21 | 20 |
| 1 | Watopia | 4487 | Always available | 34 |
Watopia is by far the most popular world. France and Makuri clearly round off the podium but are nearly indistinguishable, with the difference being on average only 129 riders in favor of Makuri. (This is despite Makuri having the novelty factor of Neokyo launching during in this period.) France’s popularity could be boosted by always being paired up with Paris, the least popular world.
In terms of number of Zwifters, the UCI worlds tend to be less popular, but New York as well, just barely ahead of them. If we further look at the true observed number of riders in Watopia when only the less popular UCI worlds are on rotation, the observed number of riders are often higher than expected from the model. This means people tend to choose Watopia in favor of Richmond, Yorkshire, and even London. However, when France and Paris are on rotation on average 109 riders less than usual selects Watopia. This is even more skewed when Makuri and New York are on rotation. On these days, nearly 200 less riders choose Watopia.
Popularity could be linked to availability as France and Paris have a high popularity and are the worlds with the fewest days in rotation in this period, less than half of Makuri. However Watopia is always present, and Makuri had the highest number of days in rotation in this period.
Small worlds with few routes could be expected to be less popular. Paris is a rather small world with only 2 routes, so it wouldn’t be expected to have the same numbers of riders before getting too crowded or people having checked off the badges. However, if we divide the number of Zwifters by the number of routes available in each world, France and Paris comes out on top, while Watopia, New York, and Makuri constitute the bottom three. This could indicate that some people to a larger degree ride the same routes over again in the smaller worlds.
So maybe different people choose different worlds? The model assumed the same curve through the 24h period for all worlds. If some worlds are more popular at specific times of day, the model will have a larger deviation between the expected and observed number of Zwifters at those periods. If we combine the two old favorite worlds Watopia and France (and they do indeed have a similar pattern), we can look for trends in the deviation from the expected (we leave out Makuri since it has Neokyo that probably have a large appeal to all Zwifters to test):
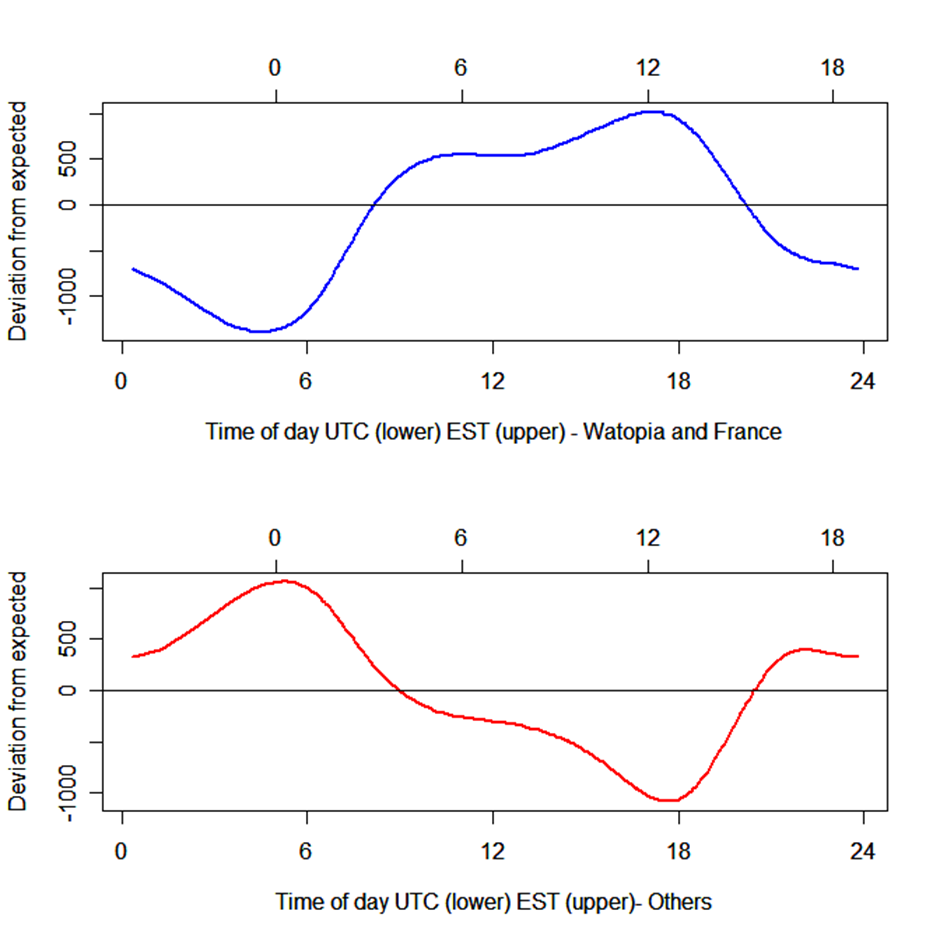
The two graphs show the trend in deviation between what is expected from the model and what is observed. A high positive number indicates a lot more people were observed in the specific world at the time than the model would expect based on a standard relationship. The observed number of riders in Watopia and France are on average nearly 1000 riders higher during the “peak” periods (1700-1800 UTC) and more than 1000 riders lower during the UTC and EST nighttime. On the other hand, people riding at UTC and EST nighttime tend to choose to ride in a world not on rotation (using world hack or participating in events).
So, France and Watopia are very popular with the typical, maybe European, Zwifter, and the realistic UCI worlds are not the most popular across any time zone. If Zwift wants to try to attract new customers, and maybe they consider Europe to be nearly fully utilized, it makes sense to expand on new fantasy worlds.
By this time I realized my hopes of riding the UCI Worlds road race course in Belgium on Zwift was diminishing…
What Effect Did the Neokyo Release Have?
So Zwift’s world expansion strategy is not a secret. They have launched Makuri Islands, added on Neokyo, and stated that they want to expand Makuri as a “sister” to Watopia. But, does launching a new world have a large effect on Zwifters’ preferences? This question is somewhat difficult to answer since I have no data on a typical autumn/winter without a “Neokyo” release. We can nevertheless try to “mine” the data for some assumptions.
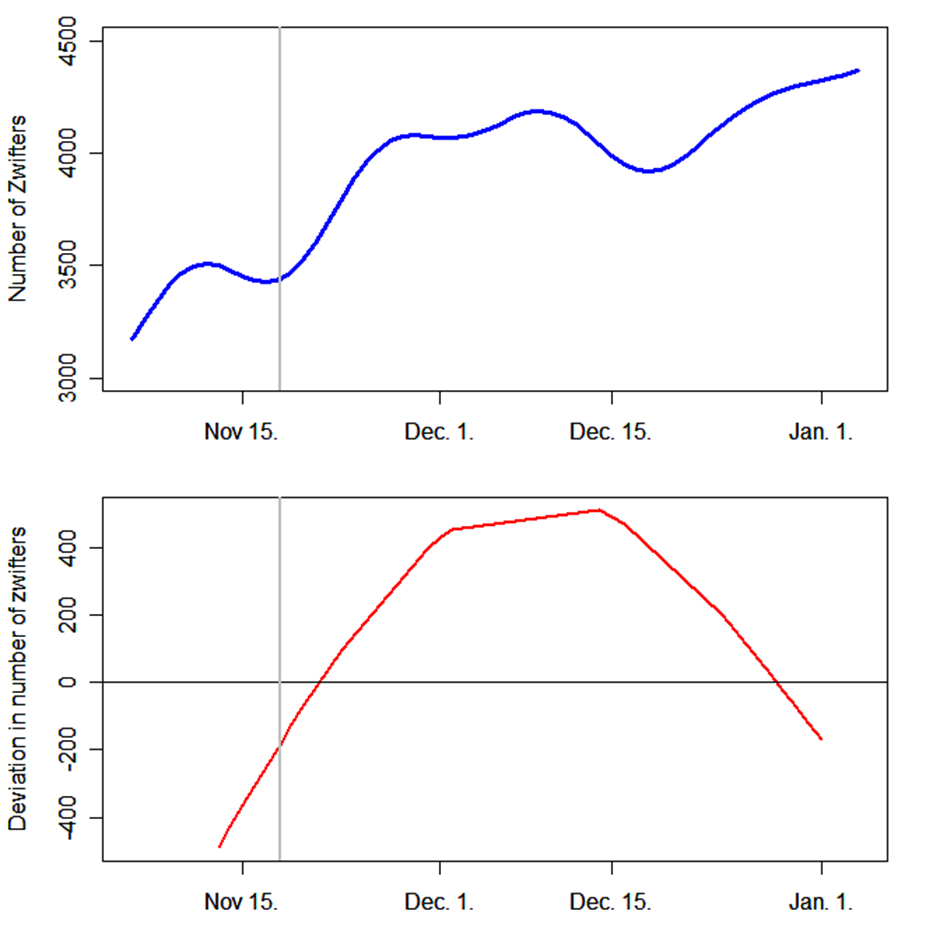
The blue curve in the top plot below is the expected number of riders in Makuri from November 5-January 5. The number of Zwifters increases in total during this period. This is probably an effect of more and more people moving from riding outside to riding indoors during winter in the northern hemisphere. The trend curve has a “two lumped bulb” starting by November 18 being the first date with numbers from Neokyo. If we imagine a linear trend through November and December, the Neokyo effect can be regarded as a surplus until the middle of December. The curve is not specific to Makuri since it’s not modeled differently for different worlds. This means the surplus is present in all worlds and could be an effect of more people logging in to Zwift in general to ride Neokyo.
To consider Makuri specifically we can look at the deviation between actually observed riders in Makuri and expected riders based on the model (with the same date effect extracted from all worlds). This is the lower curve with a red line. It becomes even more obvious that in addition to the increase of 500-600 Zwifters on a daily basis in the early Neokyo days, there were also approximately 800 more Zwifters in Makuri these days than before the release of Neokyo.
I’m a scientist and not a marketing expert, and probably Zwift has tons more customer data to plan their further strategies. But given these limited data it makes sense to keep on expanding Makuri. Although bear in mind that France seems, contrarily, to be a world with limited routes, yet still one of the most popular worlds. And personally, my favorite world is France…
Technical Notes
Data was collected from the Zwift main menu and Zwift Companion app:

The analysis is based upon the assumptions that these numbers are real and unfiltered numbers of actual Zwift users, and are not biased in any way. A total of 1144 numbers were used from 285 occasions. Observations were done from 1 to 8 times a day, with an average of 4.7 times. The range of observations per world was from 47 to 286.
Data was analyzed using a generalized additive model given by the equation:
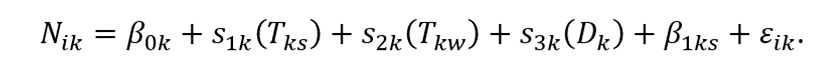
where Nik is the number of Zwifters in the i’th world at the k’th observation occasion. β0i is a world-specific intercept (corresponding to average number of Zwifters in each world), Tks is the time of day of the k’th observation occasion if the day of the k’th observation is a Saturday or Sunday. Tkw is the time of day of the k’th observation occasion if the day of the k’th observation is a weekday. Dk is the serialday of the k’th observation given by days since November 1. β1k is an offset if the k’th observation is a Saturday or Sunday.
The s1k, s2k, and s3k are specific smoothing curves (cubic splines), tailoring the effect of the covariates to the response at the different occasions through time and date. The s1k and s2k splines were modeled as cyclic to tailor the effect of the end of the 24h period to the beginning for a continuous trend. The number of knots for the smoothing curves was found using generalized cross validation. εik is the error term being identical and independently normally distributed for all worlds and at all occasions and represents deviation between model expectation and observed numbers. The model explained 90% of the variation in the data.
Questions or Comments?
Share below!